Bracket matrices stand as a fundamental pillar in mathematics and engineering, providing indispensable tools for organizing data and solving complex problems. These matrices play a critical role in diverse fields such as structural analysis, computer graphics, and beyond. For students, researchers, and professionals, mastering bracket matrices is essential for addressing intricate challenges with efficiency and precision.
This article delves into the world of bracket matrices, offering an in-depth exploration of their definitions, types, applications, and significance. By the end of this guide, you will have a solid understanding of how bracket matrices function and why they are crucial in various industries. Let’s begin by establishing a strong foundation.
Bracket matrices extend beyond theoretical concepts, finding practical applications in everyday scenarios. From solving systems of linear equations to analyzing structural frameworks, their versatility makes them an invaluable asset in modern science and technology. This article will guide you through the intricacies of this fascinating subject, ensuring a comprehensive understanding of its relevance.
Read also:Comparing The Titans Brad Brownell And Will Wade In College Basketball
Table of Contents
- What Are Bracket Matrices?
- Exploring the Types of Bracket Matrices
- Real-World Applications of Bracket Matrices
- Performing Mathematical Operations with Bracket Matrices
- Why Bracket Matrices Are Vital in Engineering
- A Historical Perspective on Matrices
- Software Tools for Working with Bracket Matrices
- Addressing Common Challenges with Bracket Matrices
- Practical Examples of Bracket Matrix Usage
- The Evolving Role of Bracket Matrices in Modern Technology
What Are Bracket Matrices?
A bracket matrix is essentially a rectangular array of numbers, symbols, or expressions arranged in rows and columns. Enclosed within brackets, this structure gives the matrix its distinctive name. These matrices serve as powerful tools for representing linear transformations, solving systems of equations, and performing various mathematical operations. The systematic arrangement of data within a bracket matrix facilitates efficient organization and manipulation, making it a cornerstone of mathematical analysis.
The dimensions of a bracket matrix are determined by the number of rows and columns it contains. For instance, a matrix with three rows and four columns is classified as a 3x4 matrix. This notation is critical for discussing the size and properties of matrices in mathematical contexts, enabling precise communication and analysis.
Key Characteristics of Bracket Matrices
- Defined by their arrangement into rows and columns
- Enclosed in brackets for clarity and ease of use
- Applied extensively in linear algebra and engineering disciplines
Exploring the Types of Bracket Matrices
Bracket matrices come in various forms, each designed for specific applications in mathematics and engineering. Understanding these types is essential for effectively leveraging their capabilities. Below, we examine some common types of bracket matrices:
Square Matrices
Square matrices feature an equal number of rows and columns. These matrices are instrumental in solving systems of linear equations and addressing eigenvalue problems, making them indispensable in mathematical and engineering contexts. Their symmetry and structure enable complex analyses and transformations.
Diagonal Matrices
A diagonal matrix is a specialized square matrix where all entries outside the main diagonal are zero. This structure simplifies numerous mathematical operations, making it a preferred choice for applications in physics and engineering. Its efficiency and clarity enhance computational processes.
Identity Matrices
An identity matrix is a diagonal matrix with ones along the main diagonal and zeros elsewhere. It serves as the multiplicative identity in matrix multiplication, ensuring consistency and accuracy in computations. Its role in mathematical operations cannot be overstated, as it acts as a fundamental reference point in matrix algebra.
Read also:The Players Championship A Clash Of Titans Between Rory Mcilroy And Jj Spaun
Real-World Applications of Bracket Matrices
Bracket matrices have a wide range of applications across multiple domains, impacting fields such as engineering, computer science, and data science. Their ability to address complex challenges makes them indispensable in these disciplines. Below, we explore some key areas where bracket matrices are widely utilized:
Engineering
Bracket matrices are pivotal in engineering for applications like structural analysis, finite element analysis, and control systems. They empower engineers to model and analyze systems with precision, ensuring the reliability and performance of structures and machines. Their versatility and precision are unmatched in solving real-world engineering problems.
Computer Graphics
In computer graphics, bracket matrices are foundational for transformations such as rotation, scaling, and translation. They enable the creation of realistic 3D models and animations, enhancing visual experiences in gaming, film, and design industries. Their role in shaping the digital world cannot be overlooked.
Data Science
Data scientists rely on matrices for data representation, machine learning algorithms, and statistical analysis. Bracket matrices provide a structured framework for managing large datasets efficiently, driving advancements in artificial intelligence and predictive modeling. Their ability to process and analyze vast amounts of data is a game-changer in the field of data science.
Performing Mathematical Operations with Bracket Matrices
Mathematical operations on bracket matrices are central to their practical application. Operations such as addition, subtraction, multiplication, and inversion form the backbone of matrix-based problem-solving. Let’s explore these operations in greater detail:
Addition and Subtraction
Matrix addition and subtraction involve combining or subtracting corresponding elements from two matrices of identical dimensions. This straightforward operation is widely employed in diverse applications, from engineering to data analysis. Its simplicity and effectiveness make it a fundamental tool in mathematical computations.
Multiplication
Matrix multiplication is a more intricate operation that entails multiplying the rows of the first matrix with the columns of the second matrix. The resulting matrix has dimensions determined by the original matrices, enabling complex transformations and analyses. Its ability to handle multi-dimensional data makes it a cornerstone of advanced mathematical techniques.
Inversion
Matrix inversion involves finding the inverse of a matrix, a critical process for solving systems of linear equations. However, not all matrices are invertible, necessitating adherence to specific conditions and the application of advanced techniques. Understanding the nuances of matrix inversion is essential for mastering matrix-based problem-solving.
Why Bracket Matrices Are Vital in Engineering
Bracket matrices are indispensable in engineering, offering a robust framework for addressing complex problems. They empower engineers to model and analyze systems with precision, ensuring the safety, efficiency, and reliability of structures and machines. Mastery of matrix manipulation and interpretation is a vital skill for engineers across various specialties.
Moreover, bracket matrices underpin the development of cutting-edge technologies, including robotics, aerospace engineering, and automation systems. Their role in computational modeling and simulation is unparalleled, solidifying their position as a cornerstone of modern engineering practices. Their versatility and precision make them an invaluable asset in advancing engineering innovations.
A Historical Perspective on Matrices
The origins of matrices trace back to ancient civilizations, where early forms emerged in Chinese and Indian mathematics. However, the formal development of matrix theory gained momentum in the 19th century, thanks to pioneering mathematicians like Arthur Cayley and James Joseph Sylvester. Their groundbreaking work laid the foundation for modern matrix algebra, which has since become integral to mathematics and engineering.
Today, matrices are studied extensively in linear algebra, a branch dedicated to vector spaces and linear transformations. The ongoing evolution of matrix theory continues to inspire advancements across scientific and technological domains, shaping the future of mathematics and engineering.
Software Tools for Working with Bracket Matrices
Several software tools are available to facilitate work with bracket matrices, making complex calculations more accessible and efficient. Popular options include MATLAB, Python (with libraries like NumPy), and Mathematica. These tools provide intuitive interfaces and robust computational capabilities, enabling users to perform matrix operations seamlessly.
For example, MATLAB is extensively used in engineering and scientific research, thanks to its comprehensive matrix manipulation functions. Python's NumPy library offers a flexible and efficient approach to handling matrices, making it a favorite among data scientists and engineers alike. Their user-friendly interfaces and powerful functionalities make them indispensable tools for matrix-based computations.
Addressing Common Challenges with Bracket Matrices
Despite their power, bracket matrices can pose challenges in certain situations. Issues such as singular matrices, numerical instability, and computational complexity may arise. Fortunately, these challenges can be effectively managed through the application of appropriate techniques and algorithms.
Singular Matrices
A singular matrix lacks an inverse, rendering it unsuitable for certain operations. To overcome this limitation, methods such as regularization or pseudoinversion can be employed, ensuring the matrix remains functional for its intended purpose. Understanding these techniques is essential for addressing potential limitations in matrix operations.
Numerical Instability
Numerical instability occurs when minor changes in input result in significant variations in output. Utilizing stable algorithms and precise numerical methods can mitigate this issue, enhancing the reliability and accuracy of matrix-based computations. Ensuring stability and precision is crucial for achieving reliable results in matrix-based problem-solving.
Practical Examples of Bracket Matrix Usage
Bracket matrices find applications in numerous real-world scenarios, demonstrating their significance across industries. Below, we highlight some examples that underscore their practical importance:
Structural Analysis
In civil engineering, bracket matrices are instrumental in analyzing the stability and strength of buildings and bridges. They assist engineers in predicting how structures will respond under various loads and conditions, ensuring safety and durability. Their role in structural analysis is indispensable in shaping modern infrastructure.
Robotics
In robotics, matrices are crucial for kinematic analysis and control systems. They enable robots to execute precise movements and interact effectively with their environment, driving advancements in automation and artificial intelligence. Their ability to enhance robotic functionality is a testament to their versatility and power.
Signal Processing
Bracket matrices play a vital role in signal processing, where they are used for filtering, compression, and transformation of signals. This application is critical in telecommunications and audio/video processing, enhancing the quality and efficiency of communication systems. Their impact on signal processing is profound, shaping the future of communication technologies.
The Evolving Role of Bracket Matrices in Modern Technology
As technology continues to evolve, the role of bracket matrices is poised to expand significantly. Innovations in artificial intelligence, machine learning, and quantum computing will likely broaden the scope of matrix applications. Researchers are actively exploring novel methods and algorithms to enhance matrix operations, making them faster, more efficient, and more versatile.
Additionally, the integration of matrices with emerging technologies such as blockchain and the Internet of Things (IoT) will unlock new possibilities for their application. The future of bracket matrix technology is bright, with countless opportunities for innovation and discovery on the horizon. Their evolving role in shaping modern technology is a testament to their enduring significance.
Conclusion
In summary, bracket matrices are a foundational concept in mathematics and engineering, offering versatile solutions to a wide array of challenges. From solving systems of equations to analyzing complex structures, these matrices provide powerful tools for addressing real-world problems. By understanding their properties and operations, professionals can unlock their full potential, driving innovation and progress in their respective fields.
We encourage you to delve deeper into the topics covered in this article and apply your newfound knowledge to practical challenges. Feel free to leave a comment or share this article with others who may find it beneficial. For more insightful content, explore our other articles on related subjects.
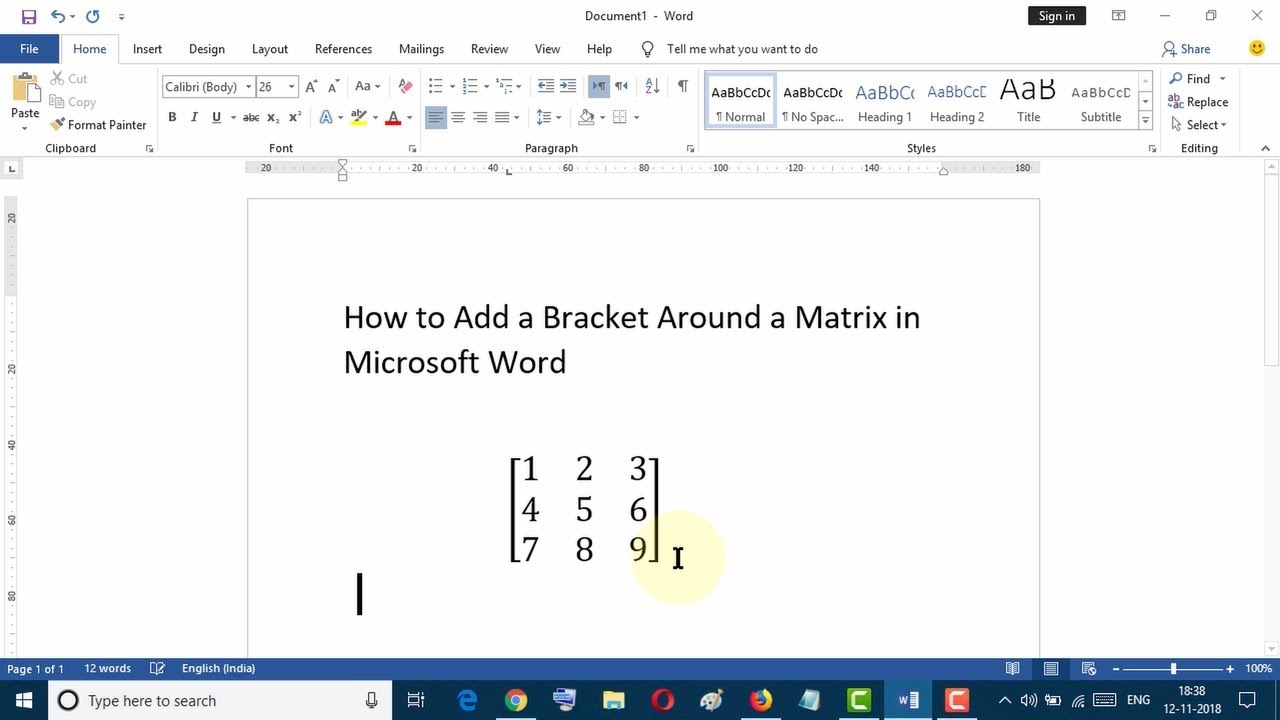
+are+enclosed+in.jpg)
